Support Vector Machines (SVM) is a supervised machine learning algorithm used primarily for classification tasks, though it can also be used for regression. It’s known for its ability to handle high-dimensional data and its efficacy in cases where the number of dimensions exceeds the number of samples.
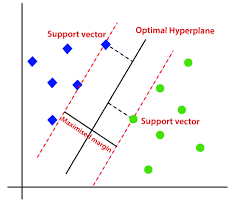
Basic Idea: SVM works by finding the hyperplane that best divides a dataset into classes. The goal is to select the hyperplane with the maximum possible margin between data points of the two classes. Data points that are closest to the hyperplane, which influence its orientation and location, are termed as “support vectors”.
Mathematical Representation: For a linearly separable dataset, the decision function of an SVM can be represented as:
f(x)=β0+β1x1+β2x2+…+βnxn
Where:
- f(x) represents the decision function.
- x1,x2,…,xn are the data attributes.
- β0,β1,…,βn are the parameters of the hyperplane.
A prediction is made based on the sign of f(x). If f(x)>0, it belongs to one class, otherwise the other class.
Maximizing the Margin: The objective of SVM is to maximize the margin between the closest points of two classes. The margin is twice the distance from the hyperplane to the nearest data point of any class. By maximizing this margin, SVM aims to generalize well to unseen data.
Kernel Trick: In many real-world scenarios, data isn’t linearly separable. SVM handles this by transforming the input space into a higher-dimensional space using a mathematical function called a kernel. In this transformed space, it becomes possible to separate the data linearly. Common kernels include:
- Linear
- Polynomial
- Radial Basis Function (RBF)
- Sigmoid
Soft Margin SVM: To handle non-linearly separable data and outliers, SVM uses a concept called “soft margin”, which allows some misclassifications in exchange for a wider margin, balancing between margin maximization and classification error.
Applications:
- Image and text classification
- Bioinformatics (e.g., classifying genes)
- Handwriting recognition
- General pattern recognition
Strengths:
- Effective in high-dimensional spaces.
- Works well when the number of dimensions is greater than the number of samples.
- Memory efficient, as it uses only a subset of the training data (support vectors) in the decision function.
Limitations:
- Not suitable for very large datasets, as the training time grows rapidly.
- Doesn’t perform well when the noise level in the dataset is high.
- Requires proper tuning of hyperparameters, like the regularization parameter, choice of kernel, and kernel parameters.
In summary, SVM is a powerful tool in the arsenal of a machine learning practitioner, particularly for classification tasks in high-dimensional spaces. Its mathematical foundation is robust, and with the right kernel and parameter choices, it can achieve impressive performance in a wide range of applications.