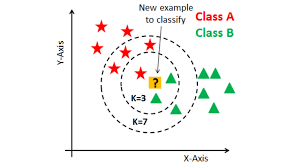
The k-Nearest Neighbors (k-NN) algorithm is a simple, intuitive, and versatile supervised learning method used for classification and regression. The core idea behind k-NN is that similar data points (based on a certain distance measure) will have similar outcomes.
How k-NN Works:
- Choosing k: Select a positive integer, typically small, as the number of neighbors to be considered. This is the ‘k’ in k-NN.
- Distance Metric: Decide on a distance metric (like Euclidean, Manhattan, Minkowski, etc.) to measure the similarity between data points.
- Finding Neighbors:
- For classification: When a prediction needs to be made for a new unseen data point, the algorithm first identifies the ‘k’ training examples that are closest to the point. It then returns the mode (most frequent) output value among them as the prediction.
- For regression: The algorithm returns the mean (or sometimes median) of the output values of the ‘k’ closest training examples.
Strengths of k-NN:
- Simplicity: The algorithm is conceptually simple and often gives reasonably competitive results without much tuning.
- No Training Phase: k-NN is a lazy learner, meaning it doesn’t “train” in the traditional sense. Instead, it memorizes the training dataset. The actual algorithm runs during the prediction phase.
- Versatility: It can be used for classification, regression, and even search (finding items most similar to a given item).
Limitations of k-NN:
- Computationally Intensive: Since k-NN requires calculating the distance of a sample to all training samples, it can be computationally expensive and slow, especially with large datasets.
- Memory-Intensive: Requires storing the entire training dataset.
- Sensitive to Irrelevant Features: The performance can degrade if there are many irrelevant features. Feature selection or dimensionality reduction techniques can help.
- Sensitive to the Scale of Data: Different features might have different scales (e.g., age vs. income). Standardizing or normalizing data is often necessary.
- Choosing ‘k’: The choice of ‘k’ (number of neighbors) can significantly affect results. A small ‘k’ can be noisy and sensitive to outliers, while a large ‘k’ can smooth out decision boundaries too much.
Practical Considerations:
- Choosing the Right Distance Metric: The default is often the Euclidean distance, but depending on the nature of the data, other distance metrics like Manhattan or Minkowski can be more appropriate.
- Weighted Voting: Instead of giving all neighbors an equal vote, one can weight their votes based on distance. Neighbors closer to the test point have more influence on the prediction.
- Efficiency Improvements: Techniques like KD-trees, Ball trees, or Approximate Nearest Neighbor (ANN) methods can speed up neighbor searches in large datasets.
In summary, k-NN is a straightforward, non-parametric method based on instance-based learning. While it’s often not the best choice for large datasets or when computational efficiency is crucial, its simplicity and versatility make it a valuable tool in the machine learning toolbox.